Numerical Analysis of Soil-Structure Interaction at Seismic Fault Pulses

Numeric Analysis of Soil-Structure Interaction at Seismic Fault Pulses

Abstraction—Numeric analysis of soil–structure systems at seismal mistake pulsations has investigated. Vibration transmissibility of the soil–structure interaction has analysed for super-structures with different aspect ratios positioned on assorted dirt types and different foundations have studied. Soil construction interaction with geometric nonlinearity has been considered with forward directionality and fling measure types of mathematical seismal mistake pulsations. It has been analyzed that nonlinear SSI is tend to magnify the acceleration responses when subjected to low frequence incident pulsations below normalized threshold frequences. These thresholds associate with dirt categorization, so that different dirt type has assorted shear moving ridge speed. With increased shear wave speed of the implicit in dirt makes the threshold frequence additions.

Order custom essay Numerical Analysis of Soil-Structure Interaction at Seismic Fault Pulses with free plagiarism report

450+ experts on 30 subjects Starting from 3 hours delivery

Get Essay Help

Keywords—Nonlinear soil–structure interaction, response analysis, seismal mistake, land daze, swaying isolation.

1. Introduction

SHOCK and quiver isolation reduces the excitement transmitted to systems necessitating protection. An illustration is the interpolation of isolators between equipment and foundations back uping the equipment. The isolators act to cut down effects of support gesture on the equipment and to cut down effects of force transmitted by the equipment to the supporting construction. Isolators act by debaring and hive awaying energy at resonating frequences of the isolation system, thereby diminishing force degrees transmitted at higher frequences. The dampers act by dispersing energy to cut down the elaboration of forces that occur at resonance [ 1 ] . The chief thought in basal isolation is to cut down the seismal responses by infixing low–stiffness, high–damping constituents between the foundation and the construction [ 2 ] . This manner, the natural period and damping of the construction will be increased, which can cut down the responses of the superstructure, particularly inter–story impetuss and floor accelerations [ 3 ] . Alternatively, base supplantings in those systems, particularly under near–fault land gestures, are increased [ 4 ] . The first concerns about this issue were arisen after 1992 Landers and so 1994 Northridge temblors, where long–period pulse–type land gestures were observed in near–fault records. Evidence show that temblor records in near–field parts may hold big energy in low frequences and can do drastic responses in base stray constructions [ 5 ] . Past surveies in the literature reveal that nonlinear soil– construction interaction ( SSI ) including foundation upheaval and dirt output can exhibit basal isolating effects due to hysteretic damping of the implicit in dirt. These effects can be important during strong land gestures when the superstructure is mounted on a shallow foundation with sufficiently low inactive perpendicular burden bearing safety factor [ 6 ] . On the other manus, geometry of the superstructure should besides enable the swaying gestures of the foundation to emerge as a singular manner of quiver in seismal public presentation of the soil–structure system. In such status, the so–called inverted–pendulum constructions [ 7 ] can profit from energy absorbing capacity of the implicit in dirt viz. swaying isolation. This context motivated Koh and Hsiung [ 8 ] , [ 9 ] to analyze base isolation benefits of 3D rocking and upheaval. In their surveies, three–dimensional cylindrical stiff block rested on a Winkler foundation of independent springs and dashpots were examined. They compared response of the theoretical account under earthquake–like excitements when the foundation was allowed to elate versus no–uplift status. It was concluded that curtailing upheaval can present higher emphasiss and accelerations inside the construction. The purpose of this paper is shock response analysis of the soil– construction systems induced by near–fault pulsations. Vibration transmissibility of the soil–structure systems is evaluated utilizing daze response spectra ( SRS ) . An in–depth parametric survey is conducted. Medium–to–high rise edifices with different aspect ratios every bit good as foundations with different safety factors located on different dirt types are studied. Two types of near–fault land dazes with different pulsation periods every bit good as pulse amplitudes are selected as input excitement. Linear versus nonlinear SSI status are considered instead and the corresponding consequences are compared.

II. N UMERICAL MODEL The soil–structure system modeled in this survey consists of

multi–story constructing constructions based on surface mat foundation located on dirt medium. Numeric theoretical account subjected to near–fault land dazes is schematically

illustrated in Fig. 1.

A. Superstructure

Shear edifice theoretical accounts are most normally used in research surveies on seismically isolated edifices. To this purpose, a generic simplified theoretical account is created to stand for a category of structural systems with a given natural period and distribution of stiffness over the height [ 10 ] . In this survey, the superstructure is a 3D shear constructing habitue in program and height to avoid the effects of geometrical dissymmetry. Requirements for including near–field effects are considered harmonizing to ASCE7–10 [ 11 ] . Dead and unrecorded tonss are assumed 600 and 200kg/m2, severally. The narrative tallness of 3.0mand figure of narratives equal to 10, 15, and 20 are selected in order to stand for medium–to–high–rise edifices that can rationally hold shallow foundations on different types of dirt medium. First–mode natural periods of fixed–base construction are 1.0, 1.5, and 2.0sfor 10– , 15– , and 20–story edifices, severally. These natural periods are consistent with approximative cardinal period expressions introduced in ASCE7–10. The analyses have been performed utilizing OpenSEES package [ 12 ] . Rayleigh theoretical account with muffling ratio equal to 5 % of critical damping is assigned to the superstructure. In this instance, superstructure elements are assumed with no ductileness and P–Delta geometrical nonlinearity is included.

FIG 1

B. Interacting System

The interacting system called infrastructure consists of soil– foundation ensemble which induces base–isolating effects to the construction. The foundation is a square mat with thickness of 1.0, 1.5, and 2.0mfor 10– , 15– , and 20–story edifices, severally. Brick elements are used to pattern the foundation. Dimensions of the foundation program were designed harmonizing to perpendicular burden bearing capacity of dirt medium. Therefore, different foundation program dimensions are calculated sing to different dirt types every bit good as different safety factors. The foundation is assumed to be inflexible and no embedment is considered in this survey. In order to see dirt effects, four types of dirt media with a broad scope of shear–wave speed (Volt) were considered to cover soft to really heavy dirt in conformity with site categorization introduced in ASCE7–10 [ 11 ] . The dirt is considered as a homogeneous half–space medium and is non modeled straight in this survey. Simplified theoretical accounts are used to enforce substructure effects including dirt flexibleness, radiation damping, tenseness cut–off, and dirt output on the foundation.

The horizontal ( sway ) electric resistances can be straight obtained utilizing Cone theoretical account expressions [ 13 ] . However, swaying and perpendicular electric resistances, because of part of foundation upheaval and dirt output nonlinear effects, could non be straight calculated utilizing lumped theoretical account in perpendicular and rocking waies. In perpendicular and swaying waies, the foundation country is discretized over a sufficient figure of nodes. The discretization of foundation program country has been done in conformity with so–called subdisk method recommended by Wolf [ 14 ] to cipher perpendicular and swaying dynamic electric resistance of dirt. In order to allow the foundation upheaval and dirt output phenomena contribute in finite component mold of soil–structure system the perpendicular nonlinear elastic–perfectly fictile spread stuff is assigned to the perpendicular contact elements.

FIG 2

III. MATHEMATICAL NEAR–FAULT PULSES Idealized pulsations, used in this survey, are described by sinusoidal maps proposed by Sasani and Bertero every bit good as Kalkan and Kunnath that represent fling measure and frontward directionality type of land gestures [ 15 ] , [ 16 ] . The mathematical preparations of the acceleration clip history of fling–step and forward–directivity pulsations are presented in ( 1 ) , and ( 2 ) , severally.

Fling–Step Pulse

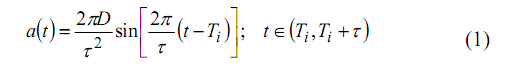
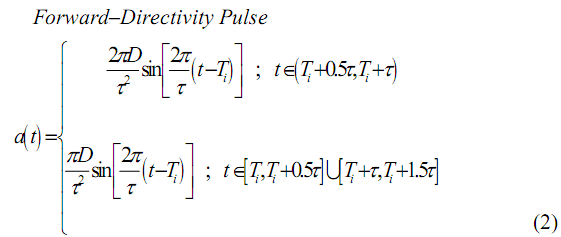
whereCalciferoldenotes the maximal amplitude of the land supplanting derived by dual clip integrating of land acceleration, ( )Ta, and so T andThyminedenote pulse period and pulse reaching clip, severally.IPulse amplitude and pulse period are the two cardinal input parametric quantities of the idealised pulsation theoretical accounts. In this research, pulse–to–fixed–base construction period ratio (ThymineT ) is assumed to fall within 0.5 to 2.5. Within this scope, existent near–field records can be replaced by idealised pulsations and outstanding belongingss of structural response are captured with sensible estimate [ 17 ] , [ 18 ] . Furthermore, pulse amplitude matching to different excitement degrees varies from moderate to really strong land gestures in this survey. For this intent, peak land speed ( PGV ) varies from 20 to 220cm/sto stand for moderate to really strong land gestures, severally. In this survey, unidirectional excitement is exerted to the base when the simplified pulse theoretical accounts of fling measure and forward directionality are used.

IV. PARAMETRIC STUDY It is good known that the response of soil–structure system

depends on geometric and dynamic belongingss of the construction and the beneath dirt. These effects can be incorporated into the studied theoretical account by the undermentioned non–dimensional parametric quantities [ 19 ] , [ 20 ] :

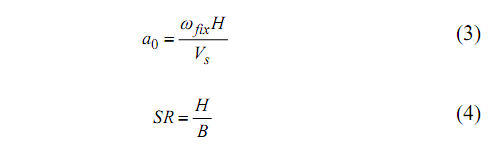
where

a0,hole,Hydrogen,Volt,Strontium, andBacillusbase for non– dimensional frequence, round frequence of the fixed–base construction, superstructure tallness, shear–wave speed of dirt, slenderness ratio, and breadth of the superstructure, in the same order. Non–dimensional frequence parametric quantity,a0, is introduced as an index for the structure–to–soil stiffness ratio. In this survey, this parametric quantity is assumed 0.25, 0.5, 1, and 2 to cover different degrees of dirt flexibleness. Harmonizing to ( 1 ) , the

a0 peers to 0.25, 0.5, 1.0, and 2.0 is matching to shear–wave speed of dirt 754, 377, 188, and 94samarium, severally.

Sing to ( 4 ) ,Strontiumparametric quantity bases for slenderness of + [ ] T + + the superstructure. In this paper, values of 2 and 4 are assigned toStrontiumparametric quantity in order to stand for low every bit good as highaandStrontium, are typically considered as the cardinal parametric quantities of the soil–aspect ratio. These two mentioned parametric quantities, 0structure system [ 19 ] . Besides, with respect to nonlinear SSI incorporated in this parametric survey, the undermentioned non– dimensional parametric quantity is besides considered:

whereNitrogen,uouN, andSFdenote the dirt bearing capacity under strictly perpendicular inactive burden, the perpendicular applied burden, and factor of safety against perpendicular burden bearing of the foundation, severally.Degree fahrenheitis set equal to 1.2, 1.85, and 2.5 to stand for severely–loaded, instead heavily–loaded, and instead lightly–loaded foundations, severally [ 21 ] .

For daze response analysis of the soil–structure system, maximal response acceleration at a givenIth narrative (MRA) is defined as time–domain utmost value of absolute response acceleration of theIth floor. Peak value ofMRAiialong tallness of the construction is defined asPMRA. This index is compared in two alternate linear every bit good as nonlinear SSI status as introduced in Fig. 2. In 2nd instance, foundation upheaval and dirt output is permitted during dynamic time–history analyses. Comparison of the two SSI status reveals swaying isolation effects of foundation upheaval and dirt output on commanding accelerations transmitted to the superstructure when subjected to near–fault land dazes. To quantify the rocking isolations effects of nonlinear SSI on commanding familial accelerations, the undermentioned index is defined:

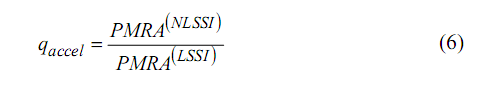
whereqacceldenotes maximal response acceleration ratio which is equal toPMRAat nonlinear SSI status,( NLSSI ) PMRA ( LSSI ) PMRAdivided by the same value at additive SSI status,

.

V. S HOCK RESPONSE SPECTRA ( SRS ) OF THE SOIL–STRUCTURE SYSTEMS Vibration transmissibility of the soil–structure systems is evaluated in this subdivision utilizing daze response spectrum. As illustrated in Figs. 3 and 4, the ordinate of each SRS curve represents theQratio as introduced in ( 6 ) . The abscissa T/Tof the SRS represents the ratio of the excitement pulsation continuanceaccelT to the natural periodThymineof the swaying isolation ( or natural period of swaying response of the foundation ) . Almost 16000 clip history analyses are performed in this survey. Consequently, the SRS braces with uninterrupted and dash lines in Figs. 3 and 4 represent mean and standard divergence ( s ) of the primary SRS curves ensemble, severally. The SRS braces are plotted with regard to different incident pulsation periods t to demo the consequence of daze strength.

In Fig. 3 the consequence of dirt type on quiver transmissibility of the soil–structure systems is investigated through comparing SRSs for different values ofa, ( 3 ) . The consequences show that nonlinear SSI is likely to magnify the acceleration responses when subjected to long–period incident pulsations with0normalized period T/Ttranscending a threshold. It is shown that this threshold T/Tcorrelatives with dirt type. In more precise words, whenalessenings ( i.e. at more dense sites ) the threshold T/Tmoves to left as displayed in Fig. 3. For case,

0

the incident pulsation with normalized period greater than the threshold, T/T= 1.25, leads to response elaboration in a 10–story edifice located on really heavy site (a=0.25 ) . On the other manus, comparing single SRS curves on each graph of Fig. 3 reveals that increasing the land daze strength consequences in steeper inclines of SRSs. This fact shows that nonlinear SSI is more activated topic to incident pulsations with greater amplitudes.

In Fig. 4 the consequence of incident pulsation type on quiver transmissibility of the soil–structure systems is examined through comparing SRSs of frontward directionality versus fling measure pulsations. The consequences show that long–period frontward directionality pulsations can ensue in important response elaboration, particularly when the pulse amplitude intensifies. In contrast, nonlinear SSI topic to short–period frontward directionality pulsations with high amplitudes can cut down the acceleration responses down to about 50 % for the 15–story edifice as presented in Fig. 4. In add-on, the two graphs of Fig. 4 depict that quiver transmissibility of nonlinear SSI is more period–dependent topic to send on directionality pulsations compared to fling measure land daze.

VI. C ONCLUSION

This paper concerns shock response analysis of the soil– construction systems induced by near–fault pulsations. To this terminal, quiver transmissibility of the soil–structure systems is evaluated utilizing daze response spectra. An in–depth parametric survey including about 16000 clip history analyses are performed. Medium–to–high rise edifices with different aspect ratios every bit good as foundations with different safety factors located on different dirt types are studied. Two types of near–fault land dazes, i.e. forward directionality and fling measure pulsations, with different pulsation periods every bit good as pulse amplitudes are selected as input excitement. Linear versus nonlinear SSI status are considered. Maximal response acceleration ratioQ

is selected as quiver transmissibility index in additive compared to nonlinear SSI status.

The consequences show that nonlinear SSI is likely to magnify the acceleration responses when subjected to long–period incident

pulsations with normalized period T/Ttranscending a threshold. This threshold T/Tcorrelatives with dirt type, so that increasing shear–wave speed of the implicit in dirt, the threshold T/T

lessenings. On the other manus, addition in land daze strength consequences in steeper inclines of SRSs, i.e. greater period dependence. Furthermore, comparing SRSs of frontward directionality versus fling measure pulsations reveals that long–period frontward directionality pulsations can ensue in important response elaboration, particularly when the pulse amplitude intensifies. In contrast, short–period frontward directionality pulsations with high amplitudes are significantly isolated. In add-on, quiver transmissibility of nonlinear SSI is more period–dependent topic to send on directionality pulsations compared to fling measure land daze.

Mentions

1. Piersol, A. G. , and Paez, T. L. , “Harris’ Shock and Vibration HandboOklahoma, ” 6^Thursdayed. , McGraw–Hill, New York, 2010.
2. Skinner, R. I. , Robinson, W. H. , and McVerry, G. H. , “An debut to seismic isolation, ” Wiley, Chichester, England, 1993.
3. Naeim, F. , and Kelly, J. M. , “Design of seismal stray constructions: From theory to pattern, ” Wiley, Chichester, England, 1999.
4. Hall, J. F. , Heaton, T. H. , Halling, M. W. , and Wald, D. J. “Near–source land gesture and its effects on flexible edifices, ”Earthquake Spectra, vol. 11, no. 4, pp. 569– 605, 1995.
5. Heaton, T. H. , Hall, J. F. , Wald, D. J. , and Halling, M. V. , “Response of high–rise and base–isolated edifices in a conjectural Mw 7.0 blind thrust temblor, ”Science, vol. 267, pp. 206–211, 1995.
6. Anastasopoulos, I. , Gazetas, G. , Loli, M. , Apostolou, M. , and Gerolymos, N. , “Soil failure can be used for seismal protection of constructions, ”Bulletin of Earthquake Engineering, vol. 8, pp. 309–326, 2010.
7. Housner, G. W. , “The behaviour of upside-down pendulum constructions during temblors, ”Bulletin of seismological society of America, vol. 53, no. 2: pp. 403–417, 1963.
8. Koh, A. , and Hsiung, C. , “Base Isolation Benefits of 3–D Rocking and Uplift. I: Theory, ”ASCE Journal of Engineering Mechanicss, vol. 117, no. 1, pp. 1–18, 1991.
9. Koh, A. & A ; Hsiung, C. “Base Isolation Benefits of 3–D Rocking and Uplift. II: Numeric Example, ”ASCE Journal of Engineering Mechanicss, vol. 117, no. 1, pp. 19–31, 1991.
10. Alhan, C. , and Surmeli, M. , “Shear edifice representations of seismically stray edifices, ”Bulletin of Earthquake Engineering, vol. 9, pp. 1643–1671, 2011.
11. ASCE/SEI 7–10, “Minimum Design Loads for Buildings and Other Structures, ” Published by American Society of Civil Engineers, 2010.
12. Fenves, G. L. , Mazzoni, S. , McKenna, F. , and Scott, M. H. , “Open System for Earthquake Engineering Simulation ( OpenSEES ), ” Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, 2004.
13. Wolf, J. P. , and Deeks, A. J. , “Foundation Vibration Analysis: a Strength–of–Materials Approach, ” Elsevier publications, 2004.
14. Wolf, J. P. , “Foundation Vibration Analysis Using Simple Physical Models, ” Englewood Cliffs ( NJ ) : Prentice–Hall, pp. 293–307, 1994.
15. Sasani, M. , and Bertero, V. “Importance of terrible pulse–type land gesture in performance–based technology: historical and critical reappraisal, ” inProc. of the 12th universe conf. on temblor technology, New Zealand, no. 8, 2000.
16. Kalkan, E. , Kunnath, S. K. , “Effects of Flinging Step and Forward Directivity on Seismic Response of Buildings, ”Earthquake Spectra, vol. 22, pp. 367–390, 2006.
17. Alavi, B. , and Krawinkler, H. , “Behavior of minute defying frame constructions subjected to near–fault land gestures, ”Earthquake Engineering and Structural Dynamics, vol. 33, pp. 687–706, 2004.
18. Sehhati, R. , Rodriguez–Marek, A. , ElGawady, M. , and Cofer, W. F. , “Effects of near–fault land gestures and tantamount pulsations on multi– narrative constructions, ”Engineering Structures, vol. 33, pp. 767–779, 2011.

Don't let plagiarism ruin your grade

Run a free check or have your essay done for you

Check my essay Hire Writer