The Influence of Temperature in the Forward Osmosis Process

Chapter Four

Mathematical Model

Chapter Four

THEORETICAL ANALYSISMA andMathematical Modeling

Purpose of the survey is to probe of temperature as a factor that influences the conveyance of H2O across the membrane in FO procedure. The steady-state theoretical accounts have been developed to foretell H2O i¬‚ux (Joule_Tungsten) as map of temperature (Thymine) and bulk concentration (C) ( i.e. Draw and Feed concentration ) . It was besides study the consequence of temperature on some belongingss, such as Solute diffusion coefficient (Calciferol_Second) , Mass transportation coefficient (K) , Permeability coefficient (A) and Solute electric resistance (K_m) .

4.1 Osmotic Pressure

The osmotic force per unit area (?) of a solution depends on the concentration of dissolved ions in solution and the temperature of solution, and can be computed by utilizing Va n't Hoff equation:

WhereNis the van’t Hoff factor ( histories for the figure of single atoms of a compound dissolved in the solution ) ,?is the osmotic coefficient,Cis the molar concentration ( molar concentration ) of the solution,Roentgenis the gas invariable andThymineis the absolute temperature of the solution. The van’t Hoff factor is introduced to cover divergences from ideal solution behaviour that include finite volume occupied by solute molecules and their common attractive force as in new wave derWaals attractive force ( Howard, 2003 ) . Table 4.1 show osmotic coefficients (?) for a figure of solutes of physiological importance ( Khudair, 2011 ) . For all solutes?depends on the substance and on its concentration. As the concentration of any solute attacks zero its value of?attacks 1. In ideal solution,?= 1 ( Glass tone, 1974 ) .

Table 4.1 Osmotic Coefficients (?) and Van’t Hoff Factor ( N ) for a Number of Solutes

Substance	Van’t Hoff Factor (N)	Osmotic Coefficients ( ? )
NaCl	2	0.93
KCl	2	0.92
HCl	2	0.95
New hampshire4Chlorine2	2	0.92
NaHCO3	2	0.96
CaCl2	3	0.86
MgCl2	3	0.89
Sodium2So4	3	0.74
MgSO4	2	0.58
Glucose	1	1.01
Sucrose	1	1.02

4.2 Concentration Polarization

4.2.1 External Concentration Polarization

Concentration polarisation ( CP ) is the accretion of solutes near the membrane surface and has inauspicious effects on membrane public presentation. The i¬‚ux of H2O through the membrane brings feed H2O ( incorporating H2O and solute ) to the membrane surface, and as clean H2O i¬‚ows through the membrane, the solutes accumulate near the membrane surface. Equations for concentration polarisation can be derived from i¬?lm theory and mass balances. Harmonizing to i¬?lm theory, a boundary bed signifiers at the surface of the membrane. Water and solutes move through the boundary bed toward the membrane surface. As H2O base on ballss through the membrane, the solute concentration at the membrane surface additions. The concentration gradient in the boundary bed leads to diffusion of solutes back toward the majority provender H2O. During uninterrupted operation, a steady-state status is reached in which the solute concentration at the membrane surface is changeless with regard to clip because the convective i¬‚ow of solutes toward the membrane is balanced by the diffusing i¬‚ow of solutes off from the surface.

A mass balance can be developed at the membrane surface as follows:

Mass accretion = mass in ? mass out ( 4.2 )

With no accretion of mass at steady province, the solute i¬‚ux toward the membrane surface must be balanced by i¬‚uxes of solute i¬‚owing off from the membrane ( due to diffusion ) and through the membrane ( into the permeate ) as follows:

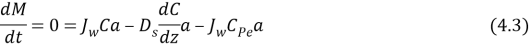
WhereMeteris mass of solute,Joule_tungstenis the experimental permeate H2O flux,Tis clip,Calciferol_Secondis the diffusion coefficient of the solute,omegathe distance perpendicular to membrane surface,C_peis the solute concentration in the permeate andE‘is the surface country of membrane. Equation 4.3 applies non merely at the membrane surface but besides at any plane in the boundary bed because the net solute i¬‚ux must be changeless throughout the boundary bed to forestall the accretion of solute anyplace within that bed ( the last term in equation 4.3 represents the solute that must go through through the boundary bed and the membrane to stop up in the permeate ) . Rearranging and incorporating equation 4.3 across the thickness of the boundary bed with the boundary conditions C ( 0 ) = C_Meterand C ( ?_Bacillus) = C_{F, cell}, where C_{F, cell}is the concentration of provender cell solution and C_Meteris the concentration at the membrane surface, are done in the undermentioned equations:

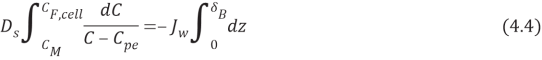
Integration outputs

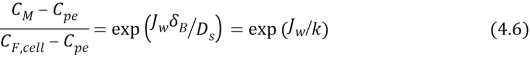
WhereKis the mass transportation coefficient and?_Bacillusthickness of the boundary bed, rearranging the equation 4.6 when utilizing the van’t Hoff equation the eventually theoretical account from the concentrative external concentration polarisation at each permeate flux, could be calculated utilizing:

Where?_{F, B}is the osmotic force per unit areas of feed solution at the majority and?_{F, m}is the osmotic force per unit areas of the provender solution at the surface membrane. Note that the advocate is positive, he pointed out that ?_{F, m}& A ; gt ; ?_{F, B}.

The draw solution in touch with the permeate side of membrane is the being diluted at the permeate membrane interface by the permeating H2O ( Moody and Kessler, 1976 ) . This is called diluted external CP. Both dilutive external CP phenomena cut down and concentrative the effectual osmotic driving force. A dilutive external CP modulus be identified as above, merely In the present instance, the concentration of the majority greater than concentration of the draw solution at the membrane surface ( i.e. ?_{D, B}& A ; gt ; ?_{D, m}) ( Cath et al. , 2006 ) :

Where?_{D, m}is the osmotic force per unit areas of the draw solution at the membrane surface and?_{D, B}is the osmotic force per unit areas of draw solution at the majority. The general equation depicting H2O conveyance in FO, RO, and PRO is ( Cath et al. , 2006 ) :

Where,Athe H2O permeableness invariable of the membrane, ? the contemplation coefficient, and a?†P is the applied force per unit area. For FO, a?†P is zero ; for RO, a?†P & A ; gt ; a?†? ; and for PRO, a?†? & A ; gt ; a?†P ( see figure 4.1 ) .

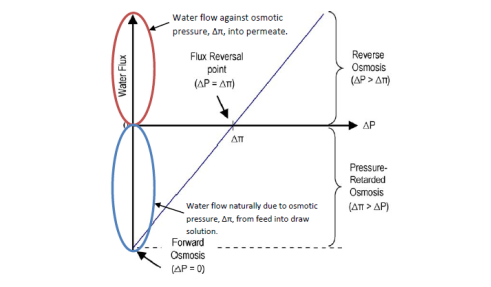
Figure 4.1 Direction and magnitude of H2O as a map of ?P.

To pattern the flux public presentation of the forward osmosis procedure in the presence of external concentration polarisation, we start with the flux equation for forward osmosis, given as

We assume that the salt does non traverse membrane, the osmotic contemplation coefficient (?) , assume equal 1. Equation 4.10 predicts Flux as maps of driving force merely in the absence dilutive external concentration polarisation or concentrative, which may to be valid merely if the permeating flux is excessively low. When higher flux rates, must be modified to include this equation both the dilutive external concentration polarisation and concentrative:

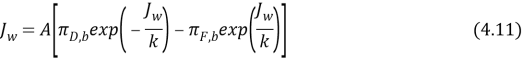
Figure 4.2 ( a ) shows this phenomenon with a dense symmetric membrane ( McCutcheon and Elimelech, 2006 ) .

4.2.2 Internal Concentration Polarization

If the porousness support bed of asymmetric membrane confronting feed solution, as is the instance in force per unit area retarded osmosis ( PRO ) , Polarization bed is established along interior of heavy active bed as H2O and solute propagate the porousness bed ( Figure 4.2 ( B ) ) . This is referred to as concentrative internal concentration polarisation, this phenomenon is similar to concentrative external concentration polarisation, except that it takes topographic point within the porous bed, and therefore, can non be underestimated by cross flow ( Lee et al, 1981 ) Obtained look patterning this phenomenon in force per unit area retarded osmosis ( Loeb et al. 1997 ) . This equation describes internal concentration polarisation ( ICP ) the effects and how it links to H2O flux, salt permeableness coefficient ( B ) and H2O permeableness coefficient:

WhereK_mis the opposition to solute diffusion within the membrane porous support bed,K_mis defined as

WhereSecondthe membrane structural parametric quantity,?_mis the thickness,?is the tortuousness and?is the porousness of the support bed,K_mis a step how easy it can be dissolved widespread support inside and outside Layer, and hence is a step of the strength of ICP. We maintain the usage of theK_mterm due to convention established in old surveies on internal concentration polarisation. Salt permeableness coefficient ( B ) is about negligible compared with the other footings in the equation 4.12. Therefore, we ignore salt flux in the way of H2O flux and any transition of salt from the permeate ( draw solution ) side ( Gray et al. , 2006 ) . Therefore, flux can be solved for implicitly from equation 4.12:

The exponential term in equation 4.14 is the rectification factor that could be considered the concentrative internal concentration polarisation modulus, defined as

Where ?_{F, I}is the osmotic force per unit area of the feed solution on the interior of the active bed within the porous support. The positive advocate indicates that ?_{F, I}& A ; gt ; ?_{F, B}, or that the consequence is concentrative. Substitute Equation 4.8 into 4.14 to obtain an analytical theoretical account for the impact of internal and external concentration polarisation on H2O flux:

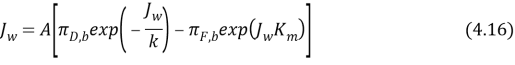
All the footings in equation 4.16 are readily determined through computations or experiments. From equation we can cipher the flux of H2O through the membrane where feeding solution is placed against asymmetric support bed and the draw solution on the active bed.

In forward osmosis applications for desalinization and H2O intervention, the active bed of the membrane faces the provender solution and the porous support bed faces the draw solution ( Kessler and Moody, 1976 ) . As H2O permeates the active bed, the draw solution within the porous infrastructure becomes diluted. This is referred to as dilutive internal concentration polarisation ( Figure 4.2 ( degree Celsius ) ) . ( Loeb et al, 1997 ) Descriptions likewise flux behaviour in the development of forward osmosis:

When presuming that B = 0 ( i.e. , the salt permeableness is negligible ) and the equation 4.17 is agreement, are acquiring an inexplicit equation for the flux of H2O permeating:

Here, ?_{D, B}is now corrected by the dilutive internal concentration polarisation modulus, given by

Where ?_{D, I}is the concentration of the draw solution on the interior of the active bed within the porous support. The negative advocate because the H2O flux is in the way off from the membrane active bed surface, In other words, the concentration polarisation consequence in our instance is dilutive, intending that ?_{D, I}& A ; lt ; ?_{D, B}by replacing equation 4.7 into 4.18, we get

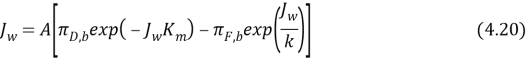
The footings in equation 4.20 are mensurable system conditions and membrane parametric quantities. Note that here ; dilutive internal concentration polarisation is coupled with concentrative external concentration polarisation, whereas in the equation 4.16, concentrative internal concentration polarisation was coupled with dilutive external concentration polarisation.

In each of these instances, the external concentration polarisation and internal concentration polarisation moduli all contribute negatively to the overall osmotic drive force. The negative part of each addition with higher flux, which suggests a self-limiting flux behaviour, this implies that increasing osmotic drive force will supply decreasing additions in flux ( Tang et al. , 2010 ) .

Figure 4.2 Illustration of osmotic driving force profiles for osmosis through several membrane types and orientations, integrating both internal and external concentration polarisation. ( a ) The profile illustrates concentrative and dilutive external CP. ( B ) PRO manner ; the profile illustrates concentrative internal CP and dilutive external CP. ( degree Celsius ) FO manner ; the profile illustrates dilutive internal CP and concentrative external CP (McCutcheon and Elimelech, 2006 ) .

In this hunt if taking transmembrane temperature difference into history, the temperature being next to membrane surface will besides differ from that in bulk solution due to the happening of heat transportation. Hence, utilizing van’t Hoff jurisprudence for computation of osmotic force per unit area requires the temperature points to be purely in line with the concentration points as

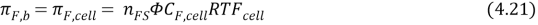
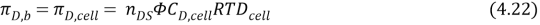
WhereC,TDandTFis the concentration, temperature draw and temperature, with the inferiors F, cell ( feed cell solution ) and D, cell ( draw cell solution ) . The theoretical account to foretell H2O i¬‚ux can be rewritten to a modii¬?ed by replacing equation 4.21 and 4.22 in 4.20, we get

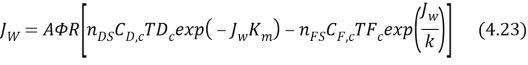
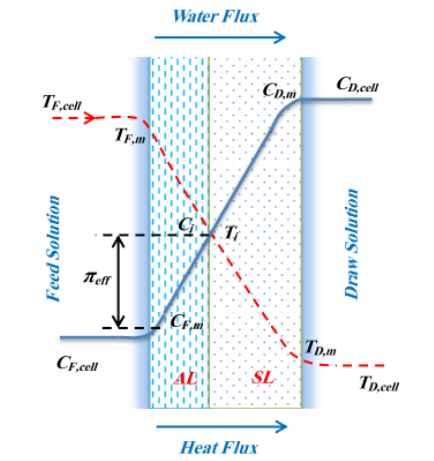Figure 4.3 gives the conventional illustration of the concentration and temperature proi¬?les in FO procedure operated under active bed – provender solution ( AL–FS ) .

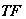
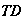
Figure 4.3Conventional diagram of mass and heat i¬‚ux proi¬?les within boundary bed and membrane during FO procedure under AL–FS manner in the presence of temperature difference ( T_{F, cell}& A ; gt ; T_{D, cell}) .

4.3 Heat Flux

Heat transportation from the solution to the membrane surface across the boundary bed in the side of the membrane faculty imposes a opposition to mass reassign The temperature at the membrane surface is lower than the corresponding value at the majority stage. This affects negatively the drive force for mass transportation. Under steady province conditions, derived from the heat balance, the heat transportation in the single compartments of system is represented by the undermentioned equation:

In which Q denotes the heat flux, and the inferiors FS – BL, m and DS – BL represent feed solution boundary bed, membrane and draw solution boundary bed. By stipulating the equation 4.24, we obtain

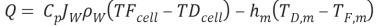
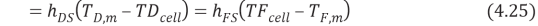
WhereHis the single heat transportation coefi¬?cient,C_Pthe specii¬?c heat of H2O,?_tungstenthe H2O denseness. Rearranging the equation 4.25 gives expressed looks of temperature near the membrane surfaces as ( Zhong et al. , 2012 )

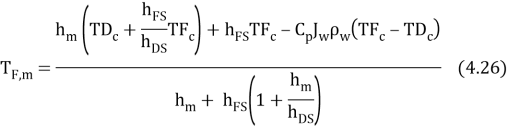
It is sensible to dei¬?ne the temperature at interface of SL and AL by averaging theThymine_{F, m}andThymine_{D, m}

4.4 Heat Transfer Coefficients

The finding of heat transportation coefi¬?cientHis developed on the footing of the correlativity between Nusselt, Reynolds and Prandtl figure ( Holman, 2009 ) .

For the laminar flow:

For the disruptive flow:

WhereNu=hL/? , Pr =C_Phosphorusµ/? ,and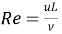.Nu is the Nusselt figure,Rheniumthe Reynolds figure andPraseodymiumthe Prandtl figure. TheC_Phosphorusis the specii¬?c heat,Literlength of the channel,µthe dynamic viscousness, and ? the thermic conduction of NaCl solution. The valueµis obtained harmonizing toµ = ??, in which?is the solution denseness, and?the kinematic viscousness. The dependance of?on temperature can be described by

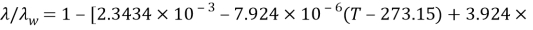
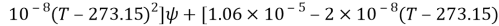
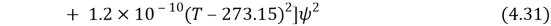
Where

And

are the thermic conduction of H2O at temperature T and 298.15 K. The heat transportation coefficientHcalculated by

Where happenNufrom equation 4.29 or 4.30

The overall heat transportation coefficientH_mof FO membrane embodies the thermic conduction of both liquid-phase H2O go throughing the micro pores and the solid-phase membrane

4.5 Mass Transfer Coefficient

The mass transportation coefficient is a map of provender flow rate, cell geometry and solute system. Generalized correlativities of mass transportation, which have been used by several writers ( Sourirajan, 1970 ) , suggest that the Sherwood figure,Sh,is related to the Reynolds figure,Re,and Schmidt figure,Sc,as: For the laminar flow:

For the disruptive flow:

Whereand.Shis the Sherwood figure,Scandiumthe Schmidt figure andvitamin D_His the hydraulic diameter, the hydraulic diameter is dei¬?ned as

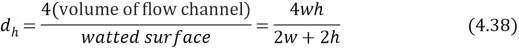
Where tungsten and h the channel breadth and channel tallness severally. The parametric quantities,Calciferol_Secondand?rely strongly on temperature, which can be quantitatively determined by empirical equations below. For aqueous electrolyte like NaCl,Calciferol_Secondvalue of the ions is presented by ( Beijing, 1988 )

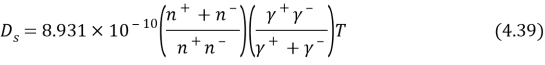
Where N^±is the absolute valley of ions ( i.e. N^±=1 ) , and ?^±is the tantamount conduction of Na⁺and Cl^-ions, estimated as

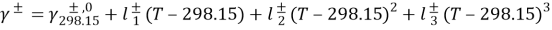
( 4.40 )

In which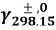( 5.1x10^-3m²/? for Na ions ; 7.64x10^-3m²/? for chloride ions ) is the mention tantamount conduction at 298.15 K ; temperature coefficient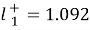,,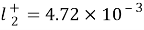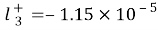forSodium⁺, and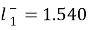,,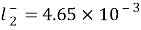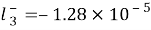for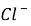, severally.

The empirical equations were employed to gauge kinematic viscousness of NaCl solution as

Whereis the H2O viscousness at temperature T, expressed as

In whichvitamin E= 0.12,degree Fahrenheit= -0.44,??-ˆ= -3.713,I=2.792 are the fitting parametric quantities,C_Secondthe NaCl molar concentration, andThymine_Roentgenthe normalized temperature.

There is besides another manner to cipher diffusion coefficient in the liquid stage of a dilute solution can be estimated by the Stokes – Einstein equation if the solute radius is clearly larger than the solvent radius

WhereK_Bacillusis the Boltzmann invariable, T ( K ) is the absolute temperature, µ is the dynamic viscousness of the liquid and R_Ois the radius of the solute. To cipher diffusion coefficients in aqueous solutions predict that diffusion coefficients really linearly with temperature and reciprocally with viscousness. Indeed, harmonizing to Li and Gregory, ( 1974 ) .

In instance of the stokes – Einstein relation the diffusion coefficientD ( T )at a temperatureThymineis given as

Where D( T_O)is the diffusion coefficient at a mention temperatureThymine_Oandµ ( T )andµ ( T_O)are the dynamic viscousnesss at temperaturesThymineandThymine_O, severally. Note that temperatures are given in Kelvin.

Finally the mass transportation coefficient K calculated by

WhereShdiscovery from equation 4.36 or 4.37

4.6 Water Permeability Coefficient

The equation ciphering pure H2O permeableness coefi¬?cient A for FO procedure is derived from the theoretical account ; thereby the H2O i¬‚ux of rearward osmosis procedure is predicted ( Baker, 2004 )

WhereC_tungstenis the H2O molar concentration,Volt_tungstenthe molar volume of H2O,Calciferol_effthe effectual H2O molecule diffusivity within the pores of active bed of the FO membrane

Wherevitamin D_Second( 4A^O) andvitamin D_Phosphorus( 7.2A^O) are the diameter of H2O molecule and pore, and D the evident diffusivity, which is given as

Along with H2O dynamic viscousness ( µw ) predicted by

There is besides another manner to cipher membrane permeableness ( A ) i¬‚at-sheet bench-scale RO trial system was used to find the H2O permeableness coefi¬?cient ( A ) of the CTA membrane. A membrane voucher holding an effectual surface country of 64 centimeter²was the active bed of the membrane confronting the provender solution. Mesh spacers placed in the provender channel enhanced the turbulency of the ultrapure H2O provender watercourse. A hard-hitting positive supplanting pump was used to recirculate the provender solution at 12 L/h.

The FO membrane H2O permeableness coefi¬?cient ( A ) was determined utilizing ( Lee et al. , 1981 ) .

Where ?? is the osmotic force per unit area difference across the membrane and ?P is the hydraulic force per unit area difference across the membrane.

Because ultrapure H2O was used as the provender solution, ?? was zero during the experiments. Pressure was increased from 1 saloon to 2 saloon. Pressure was held changeless at each increase for continuance of 3 h. Water i¬‚ux through the membrane was calculated based on the increasing weight of the permeant H2O on an analytical balance. The temperature was held changeless at 25^OC. See figure 4.4

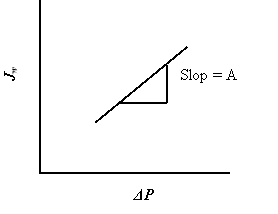
Figure 4.4 Flux vs. force per unit area and the swill is representedH2O permeableness coefi¬?cient ( A ) .

4.7 Recovery Percentage

The recovery factor measures how much of the provender is recovered as permeate. It is reported as a per centum ( Al-Alawy, 2000 ) . The recovery of the membrane was calculated by spliting the overall of permeate rate by the provender rate solution. Recovery, or transition, is defined by:

WhereVolt_Phosphorusis the overall permeate volume andVolt_Fis the provender volume solution.

Figure 4.5 the flow chart of patterning FO H2O flux at different temperature matrixes.

1

Cite this Page

The Influence of Temperature in the Forward Osmosis Process. (2018, Jul 23). Retrieved from https://phdessay.com/the-influence-of-temperature-in-the-forward-osmosis-process/

copy to clipboard