Colorflex and temperature measurement in coffee production
Coffee industry represents the colour of roasted java as a individual value such as SCAA or HCCI colour criterion. PT. ACI uses Colorette 3b with a graduated table of 0 to 200 to stand for the colour between visible radiation into dark. This instrument can non mensurate the debasement of java colour during roasting which has a wider colour scope. This survey applied the ColorFlex that is designed with CIE criterion colour measuring by using a particular visible radiation beginning and a standard perceiver angle. The samples were measured with the standard visible radiation beginning of Daylight ( D65 ) and the normal observer angle of 100. In some instances, the colour is frequently represented as chrome values but in this survey we used the colour difference ( & A ; Delta ; E ) which was calculated from the CIEL*a*b* co-ordinate to stand for the java colour. The CIEL*a*b* is calculated with following equation.
where Ten, Y, Z as the Tristimulus values ;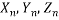 are changeless values of 94.811, 100, and 107.3 severally matching to the light and observation angles. The co-ordinate of L* describe the degree of brightness, a* is the colour strength of ruddy ( + ) to green ( - ) , and b* describe the strength of yellow ( + ) to blue ( - ) . The & A ; Delta ; E is defined as follows.
are changeless values of 94.811, 100, and 107.3 severally matching to the light and observation angles. The co-ordinate of L* describe the degree of brightness, a* is the colour strength of ruddy ( + ) to green ( - ) , and b* describe the strength of yellow ( + ) to blue ( - ) . The & A ; Delta ; E is defined as follows.
where the indexes of 2 and 1 represent the object being measured and the mention. By presuming a black organic structure as mention ( the colour values are severally close to nothing ) , the & A ; Delta ; E is merely determined by the colour of the object. Therefore, eq.5 can be written as follows.
Order custom essay Colorflex and temperature measurement in coffee production with free plagiarism report
 450+ experts on 30 subjects
450+ experts on 30 subjects
 Starting from 3 hours delivery
Starting from 3 hours delivery
The relationship between the & A ; Delta ; E measured by the ColorFlex with colour value provided by Collorete 3b for the same sample. The consequence indicates a additive relationship ( high value of correlativity coefficient ) between both graduated tables and hence, this ColorFlex can be applied to mensurate the colour of roasted java.
The figure presents informations of detector response, grain colour, and points of three roast-degrees ( light-medium-dark ) for each measuring. The response of detectors was so processed into olfactory property forms captured at 3 min interval harmonizing to the observation clip of the colour parametric quantity. After that, the olfactory property form was analyzed to the colour and temperature informations. The same method was applied to the olfactory property form at the three critical points.
The effectual detector response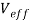 was presented as a series of an effectual electromotive force detector at t-time after it was subtracted with an initial electromotive force for a mention. In this instance, the response of each detector in the first measuring ( t=180 s ) was considered as the mention. The
was presented as a series of an effectual electromotive force detector at t-time after it was subtracted with an initial electromotive force for a mention. In this instance, the response of each detector in the first measuring ( t=180 s ) was considered as the mention. The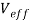 can be written as follows.
can be written as follows.
PCA is a statistical method that is widely used for analysing the distribution of an experimental information. PCA is besides known as the Karhunen-Loeve or Hotelling transmutation which is one based on statistical analysis of extraneous transmutation for change overing a set of experimental informations which may incorporate of correlative variables into a set of new informations which contain of non linearly correlative variables known as chief constituent ( Personal computer ) . Personal computer on the first sequence contains the greatest variant value of the experimental information followed by the 2nd Personal computer, the 3rd, and so on. Mathematically, PCA algorithm can be solved by the method of Covariance. The covariance matrix of an experimental information is defined as follows.
where Ten is the matrix of the experimental informations with size of M x N, M is the figure of informations variable ( e.g. figure of detectors ) and N is the figure of the information, I and J are the index of the informations variable and the figure of experimental informations,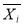 is the norm of the informations for each variable,
is the norm of the informations for each variable,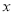 is a individual vector of the form informations containing of the M variable, and
is a individual vector of the form informations containing of the M variable, and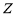 is the nothing mean informations. Based on Eq. 8, the covariance matrix of C is an extraneous matrix with size of M x M. PCA algorithm dramas to happen the characteristic root of a square matrix (
is the nothing mean informations. Based on Eq. 8, the covariance matrix of C is an extraneous matrix with size of M x M. PCA algorithm dramas to happen the characteristic root of a square matrix ( ) and eigenvector (
) and eigenvector (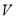 ) of the matrix, which can be described as follow.
) of the matrix, which can be described as follow.
Eq. 9 can be solved by the Jacobian method. The obtained characteristic root of a square matrix represents the figure of discrepancies of informations stored in each corresponding eigenvector. The eigenvector is besides called as a characteristic vector being used to transform the observation informations. Vector Personal computer as the consequence of this transmutation can be calculated by the undermentioned equation.
where I is the index of the input vector variable, J is the index of Personal computer matching to the sequence of the characteristic vector. The distribution of the experimental informations can be visualized by plotting the Personal computers on the Cartesian vector graph for either 2D or 3D. The distribution of the experimental information is visualized on the graph with the degree depending on the sum of discrepancy from the selected Personal computers. In many instances, the usage of the top of 2 or 3 Personal computers already represents more than 80 % of the discrepancy of the analyzed information, and so that the distribution have reflected the existent distribution of the informations.
The colour profile tends to travel down demoing the colour debasement from the yellow-green colour for green bean into the brownish colour for roasted bean. This alteration indicates an addition in degree of roasted java along with the length of the procedure. In add-on gives information that shows the colour alteration of a downward tendency, the chart besides provides scope of the colour values at each trying. From the consequence, it appears that the scope colour value of the grain in the early stages tends to be little for all replicates. The longer roasting clip be givening to widen the scope of colour values indicates a difference degree of adulthood of the roasted java. A similar consequence is besides performed by the profile of temperature. In the early stages, the roaster membranophone was set at the same temperature of 2000C before the java sample was inserted. The temperature will drop about 40-500C in the beginning of roasting and so easy traveling up once more as the clip of roasting occur.
This is apprehensible because of the dramatic differences between roaster room temperature with the get downing java grain. At that point, the heat will be absorbed rapidly into the java grains. Although the warming component stays on but this soaking up is greater than the supply of thermal. In short, this temperature is profiled by a lessening in the initial stages so the procedure will slowly rise until it reaches a temperature of 2000C. In line with old consequences with the ascertained scope of temperature values for each sampling clip, it is seen an addition in the scope of values.
This shows that even though the procedure fixes the initial conditions of roasting, uses top-quality java bean, and adjusts an equal blower gap but the ripeness of the java grains is non equal for each sampling clip among experiment reproductions. These consequences prove that the both parametric quantity can non be used to reflect the joint degree though with homogenous stuffs. Furthermore, in existent conditions, the java grains as natural stuff in industry are obtained from providers with heterogenous for footings of quality, shelf life, wet content, and denseness. Therefore, the both parametric quantities have restriction to be used as an index of the degree of roasted java.
Cite this Page
Colorflex and temperature measurement in coffee production. (2018, Aug 04). Retrieved from https://phdessay.com/colorflex-and-temperature-measurement-in-coffee-production/
Run a free check or have your essay done for you


