Design of Single Mode TE Mode Optical Polarizers
Design of Single manner TE mode optical Polarizer Using Silicon Oxynitide multilayed wave guide
Abstraction-A Si oxynitride ( SiON ) guided movie is used as multilayered wave guide and utilizing transportation matrix method.We propose the application of wave guide as a TE-Pass polarizer and TM-Pass polarizer holding a passband in the 3rd optical communicating window of 1550 nanometer. Polarizer is cardinal constituent for devices which require a individual polarisation for their operation. Most of the polarizers use metal clad wave guides with proper thickness and refractile index of screen and substrate.
Index Terms— Optical Polarizer, Multi-layered wave guide, TE manner, Silicon oxynitride
Order custom essay Design of Single Mode TE Mode Optical Polarizers with free plagiarism report
 450+ experts on 30 subjects
450+ experts on 30 subjects
 Starting from 3 hours delivery
Starting from 3 hours delivery
Introduction
Optical wave guide: An optical wave guide is a physical construction that guides electromagnetic moving ridges in the optical spectrum. Common types of optical wave guides include optical fiber and rectangular wave guides.
To manufacture a planing machine wave guide ( Fig.1 ) , normally a movie ( refractile index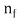 ) , with a screen bed ( refractile index
) , with a screen bed ( refractile index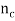 ) , is grown on a substrate ( refractile index
) , is grown on a substrate ( refractile index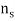 ) such that
) such that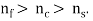 Such wave guides are known as asymmetric wave guides. For symmetric wave guide, the screen and substrate are fabricated with same stuff and the refractile indices are equal, i.e.
Such wave guides are known as asymmetric wave guides. For symmetric wave guide, the screen and substrate are fabricated with same stuff and the refractile indices are equal, i.e.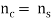 .
.
If there are more than one bed between Cover and Substrate, so such type of optical wave guides are known as Multilayer Waveguide.
In a multi-layered wave guide, we have pick to manufacture as many beds as we required. We can choose the thickness of the beds and the type of the stuff harmonizing to our demand.
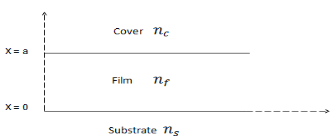
Fig. 1 Geometry of 3-layer wave guide construction
For a N-layer construction, theDefineframe receives the vacuity wavelength, the refractile index valuesns ( substrate ) , n1, ... , nN ( interior beds 1 to N ) , nc ( screen ) , and the thicknessest1, ... , tNof the interior beds. All dimensions are meant in microns. The figure illustrates the relevant geometry:
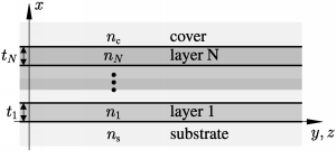
Fig.2 Geometry of multilayer wave guide construction
Multilayer wave guides are used in the execution of a assortment of optical devices including semiconducting material optical masers, modulators, wave guide polarisers, Bragg reflectors, and directional couplings.
During the last 20 old ages, many efforts have been made to work out the moving ridge equation for the propagating manners in a general, lossless or lossy multilayer wave guide, in such a manner as to ease the design and optimisation of the above optical devices.
TE-Pass Polarizer
Silicon oxynitride ( SiON ) planar waveguide construction can be fabricated by utilizing plasma enhanced chemical vapor deposition ( PECVD ) . In this technique oxidization reaction is initiated by plasma instead than utilizing external warming beginning. Other techniques are runing technique, vapour stage deposition technique but CVD technique is superior. These wave guides find assorted applications in optical communicating particularly as wavelength filter, microresonator, modulator, polarisation splitter and 2nd harmonic generator.
A SiON guided movie is used as multilayered wave guide and utilizing transportation matrix method we propose the application of wave guide as a TE-Pass polarizer and TM-Pass polarizer holding a passband in the 3rd optical communicating window of 1550 nanometer. Polarizer is cardinal constituent for devices which require a individual polarisation for their operation. Most of the polarizer usage metal clad wave guides with proper thickness and refractile index of screen and substrate.
Multilayer wave guides are used in the execution of a assortment of optical devices including semiconducting material optical masers, modulators, waveguide polarizer, Bragg reflectors, and directional couplings.
We propose a multilayered SiON wave guide fabricated on substrate and has metal as screen is shown in fig 2. The pick of SiON is made for its extremely desirable characteristics such as low interpolation loss, broad scope of refractile index tailoring and realisation of compact devices because of its low bending loss. The present constellation of optical polarizer will happen applications in incorporate optical circuits, signal processing from fiber ocular detectors and fiber gyroscopes. For the analysis of the wave guide we have used the transportation matrix preparation.
as screen is shown in fig 2. The pick of SiON is made for its extremely desirable characteristics such as low interpolation loss, broad scope of refractile index tailoring and realisation of compact devices because of its low bending loss. The present constellation of optical polarizer will happen applications in incorporate optical circuits, signal processing from fiber ocular detectors and fiber gyroscopes. For the analysis of the wave guide we have used the transportation matrix preparation.


Fig.3 Geometry of multilayer wave guide construction
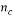 = refractile index of the screen
= refractile index of the screen
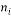 = refractile index of the movie i=1, 2………r
= refractile index of the movie i=1, 2………r
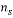 = refractile index of the substrate
= refractile index of the substrate
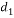 = thickness of the movie bed in micrometer
= thickness of the movie bed in micrometer
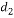 = thickness of the movie bed in micrometer
= thickness of the movie bed in micrometer
Figure 1:Formulation
For the computation of extension invariable and ensuing extension manner profile of multi-layered wave guide, there are following methods: -
1. Disturbance Method ( 4-layer )
2. Newton’s Method
3. Mode-matching method ( 5-layer construction )
4. Transfer Matrix Formulation
5. Argument Principle Method
The disturbance method for a lossless 5-layer construction, for a lossy 4-layer construction, and for a metal-clad wave guide was used to find the extension invariables and the ensuing propagating manner profiles. Newton’s method was used for metal-clad wave guides where the derived function of the scattering equation can be obtained analytically. A graphical method, every bit good as formal electromagnetic analysis methods such as the mode-matching method, was besides used. The disturbance method every bit good as Newton’s method can non easy be extended to multilayer constructions, since their attack is analytic and the expression involved become cumbersome.
None of the above methods can easy foretell the figure of propagating manners supported by the multilayer construction. This is a serious job since there is no manner of cognizing when to halt seeking for new propagating manners or even if the wave guide really can back up any manner at all. In fact, an extra analysis must be used to find the figure of guided manners before using the zero-searching techniques. Even if the figure of bing propagating guided manners is given, there is no verification that all the manners will be found. All the above mentioned methods have serious jobs in turn uping closely spaced roots. Furthermore, all of them need an initial estimate near to the existent nothing. This initial estimation may be hard to happen, particularly for high-loss propagating manners where the popular disturbance method does non use. The method which we are utilizing, is based on complex figure theory. It is capable of happening the nothing or poles of any analytic map in the complex plane. The scattering equation of a general multilayer wave guide is formed via the construct of thin-film transfer-matrix theory. After its uniqueness points are observed, the complex plane is divided into parts where the scattering equation is analytic, and all the zeros inside each part are found. In add-on, the method provides the figure of nothing or poles in each part. The transfer-matrix analysis provides an easy preparation of the multilayer construction job. The method will be presented for TE manners but the extension to TM manners is straightforward.
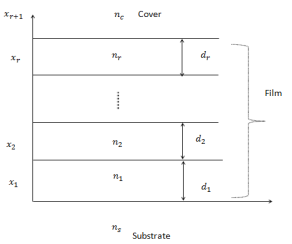
Fig.4 TE-Pass Polarizer
A multilayer nonmagnetic slab wave guide construction( µ=µO) ,is shown in Fig. 2. The refractile index,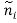 ,of the IThursdaybed can be complex in general, i.e. ,
,of the IThursdaybed can be complex in general, i.e. ,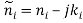 ,where
,where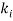 ,is the extinction coefficient of the IThursdaybed and I = 1.. . ..randRis the layer figure. For aTelluriummanner propagating in the+
,is the extinction coefficient of the IThursdaybed and I = 1.. . ..randRis the layer figure. For aTelluriummanner propagating in the+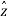 way in the IThursdaybed, (tenI? x ? xi+1) , the electric field is
way in the IThursdaybed, (tenI? x ? xi+1) , the electric field is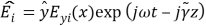 ,and the magnetic field in the same bed is
,and the magnetic field in the same bed is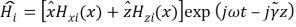 where
where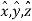 are the unit vectors in theten, Y, omegaway, severally,
are the unit vectors in theten, Y, omegaway, severally,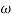 is the radian frequence, and
is the radian frequence, and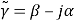 is the complex extension invariable with
is the complex extension invariable with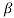 and
and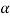 the stage and the fading invariables severally
the stage and the fading invariables severally
2.1 TE Mode
A multilayer nonmagnetic slab wave guide construction( µ=µO) ,is shown in Fig. 3. The refractile index,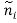 ,of the IThursdaybed can be complex in general, i.e. ,
,of the IThursdaybed can be complex in general, i.e. ,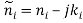 ,where
,where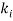 ,is the extinction coefficient of the IThursdaybed and I = 1.. . ..randRis the layer figure. For aTelluriummanner propagating in the+
,is the extinction coefficient of the IThursdaybed and I = 1.. . ..randRis the layer figure. For aTelluriummanner propagating in the+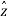 way in the IThursdaybed, (tenI? x ? xi+1) , the electric field is
way in the IThursdaybed, (tenI? x ? xi+1) , the electric field is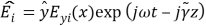 ,and the magnetic field in the same bed is
,and the magnetic field in the same bed is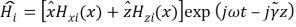 where
where are the unit vectors in theten, Y, omegaway, severally,
are the unit vectors in theten, Y, omegaway, severally, is the radian frequence, and
is the radian frequence, and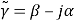 is the complex extension invariable with
is the complex extension invariable with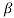 and
and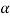 the stage and the fading invariables severally
the stage and the fading invariables severally
By utilizing Maxwell’s differential equations, we get
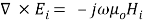
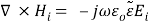
For TE manner,
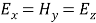 = 0, merely
= 0, merely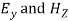 constituents will show.
constituents will show.
So by work outing above two Maxwell’s equations, we get
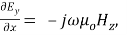 ( 1 )
( 1 )

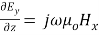 ( 2 )
( 2 )
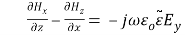 ( 3 )
( 3 )
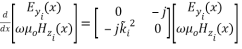 ( 6 )
( 6 )
where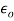 is the freespace permittivity,
is the freespace permittivity,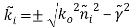 and
and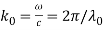 , c is the velocity of the visible radiation in the freespace and
, c is the velocity of the visible radiation in the freespace and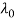 is the freespace wavelength. The electric and magnetic The Electric and Magnetic digressive Fieldss within the IThursdaybed are solutions of above equation, and can be written as
is the freespace wavelength. The electric and magnetic The Electric and Magnetic digressive Fieldss within the IThursdaybed are solutions of above equation, and can be written as
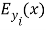 = AI
= AI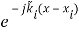 + BI
+ BI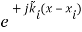 ( 7 a )
( 7 a )
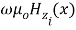 =j
=j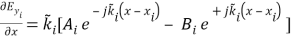 ( 7 B )
( 7 B )
When we apply boundary status at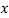 =
=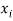 in equations ( 7 a ) and ( 7 B ) , so we will acquire
in equations ( 7 a ) and ( 7 B ) , so we will acquire
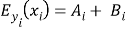
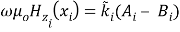 ( 8 )
( 8 )
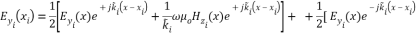
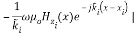
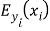 =cos [
=cos [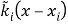 ]
]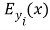 +
+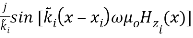 ( 10 a )
( 10 a )
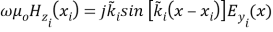
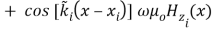 ( 10 B )
( 10 B )
Adding equation ( 10 a ) and ( 10 B )
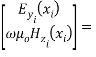
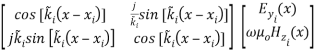 ( 11 )
( 11 )
Using the continuity of the digressive Fieldss at any layer interface in the multilayer construction, the Fieldss digressive to the boundaries at the top of the substrate bed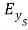 ,
,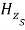 and at the underside of the screen bed
and at the underside of the screen bed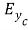 ,
,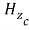 , are related via the matrix merchandise
, are related via the matrix merchandise
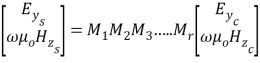
=[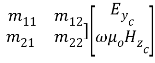 ( 12 )
( 12 )
Where
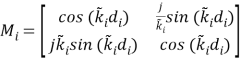 for one = 1,2……….. , R( 13 )
for one = 1,2……….. , R( 13 )
Are the transportation matrices for all of theRbeds holding thickness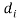 . For propagating manners, the digressive Fieldss at the boundaries must be exponentially disintegrating holding the signifier
. For propagating manners, the digressive Fieldss at the boundaries must be exponentially disintegrating holding the signifier
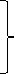
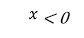
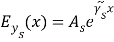 ( 14 )
( 14 )
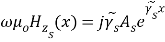
And
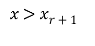
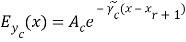 ( 15 )
( 15 )
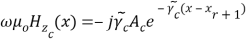
Where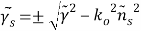 ,
,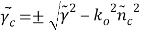
From equation ( 12 ) , we get
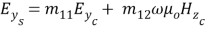
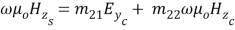
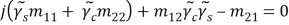
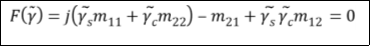
The extinction ratio ( PER ) is defined as the ratio of power staying ( at the end product terminal ) in the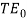 manner (
manner (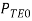 ) to the power staying ( at the end product terminal ) in the
) to the power staying ( at the end product terminal ) in the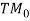 manner (
manner (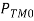 ) , expressed in dBs. In add-on, the interpolation loss ( PIL ) is defined as the power loss associated with the
) , expressed in dBs. In add-on, the interpolation loss ( PIL ) is defined as the power loss associated with the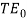 manner. Frankincense:
manner. Frankincense:
PER= 10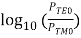
PER=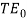 Loss in dubnium?
Loss in dubnium?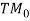 Loss in dubnium
Loss in dubnium
PIL= 10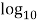 (
(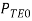 )
)
PIL=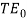 Loss in dubnium
Loss in dubnium
The above equations assume that the input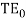 manner has unit power at the input terminal of the polarizer. In order to hold a good TE-pass polarizer, we require the power staying in the desired
manner has unit power at the input terminal of the polarizer. In order to hold a good TE-pass polarizer, we require the power staying in the desired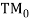 manner at the end product terminal of the polarizer to be every bit high as possible. Hence a low value of PIL is desirable. The effectivity of the polarizer in know aparting against the transition of the
manner at the end product terminal of the polarizer to be every bit high as possible. Hence a low value of PIL is desirable. The effectivity of the polarizer in know aparting against the transition of the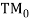 mode comparative to the
mode comparative to the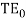 manner is measured by the PER parametric quantity. Therefore, this parametric quantity should be every bit high as possible. Hence, we require a high PER and at the same time a low PIL.
manner is measured by the PER parametric quantity. Therefore, this parametric quantity should be every bit high as possible. Hence, we require a high PER and at the same time a low PIL.
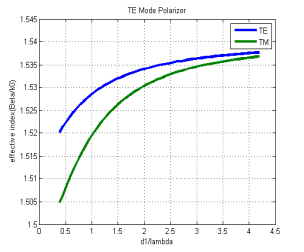
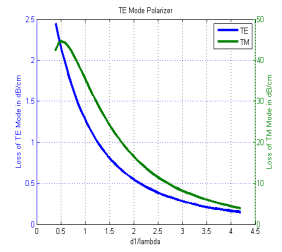
Figure 5.1: Effective index w.r.t.normalized movie Figure 5.2: Loss w.r.t.normalized movie bed
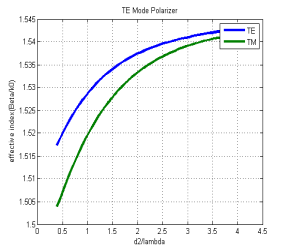
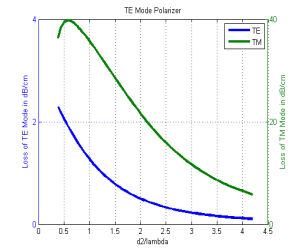
Fig. 5.3: Effective index w.r.t.normalized movie bed Fig. 5.4: Loss w.r.t.normalized movie bed
Decision
First of wholly, we have checked the map of TE manner by utilizing transportation matrix method [ 2 ] . The value of stage changeless and fading invariable for 6-layer Lossy Dielectric Waveguide are available. The available informations were calculated by the method of Argument Principle ( APM ) .
Transportation Matrix method has been used to analyze a four superimposed waveguide dwelling of SiON as guiding movie. On this footing, we have designed TE base on balls polarizer. The scope of SiON movie thickness was estimated so that merely the cardinal pervert TE0is supported. The computations showed that in the thickness scope of 0.7µm -2.2 µm of SiON, the wave guide supports merely TE0manner.
In TE manner base on balls polarizer, the loss of TE manner is in the scope of 0.2 – 2.5 dB/cm and for TM mode its scope is 40 - 45 dB/cm, which rather higher in comparing to TE manner. So in this type of constellation of four bed wave guide, merely TE manner will go through.
Mentions
[ 1 ] Vishnu Priye, Bishnu P.Pal, and K.Thyagarajan, “ Analysis and Design of a Novel Leaky YIG Film Guided Wave Optical Isolator, ”J. Lightwave Technol. , vol. 16, No.2, February 1998
[ 2 ] Anemogiannis and E.N.Glytis, “Multilayer waveguides: Efficient numerical analysis of general constructions, ”J. Lightwave Technol. , vol. 10, pp. 1344-1351, 1992
[ 3 ] M.Ajmal Khan and Hussain A. Jamid, “ TE/TM Pass Guided Wave Optical Polarizer” , IEEETEM2003
[ 4 ] H.Kogelnik, Theory of Optical Waveguides in Guided-wave Optoelectronics, T. Tamir, Ed. New York: Springer-verlag, 1988
[ 5 ] AJOY K. GHATAK, K. THYAGARAJAN, AND M. R. SHENOY Numerical Analysis of Planar Optical Waveguides Using Matrix Approach
[ 6 ] Ajoy Ghatak and K.Thyagarajan, “ Optical Electronics’’ , Cambridge University Press
[ 7 ] Joseph A Edminister and Vishnu Priye, “Electromagnetics Schaum’s Outline, Tata MacGraw Education Private Limited”
Cite this Page
Design of Single Mode TE Mode Optical Polarizers. (2018, Jul 21). Retrieved from https://phdessay.com/design-of-single-mode-te-mode-optical-polarizers/
Run a free check or have your essay done for you


